Y=x^2-4x 1 parabola 249151

Step 1 use the (known) coordinates of the vertex, ( h, k), to write the parabola 's equation in the form y = a ( x − h) 2 k the problem now only consists of having to find the value of the coefficient a Step 2 find the value of the coefficient a by substituting the coordinates of point P into the equation written in step 1 and solving The parabolas y^2 = 4x and x^2 = 4y divide the square region bounded by the lines x = 4, y = 4 The parabolas y2 = 4x and x2 = 4y divide the square region bounded by the lines x = 4, y = 4 and the coordinate axes If S1, S2 and S3 are respectively the areas of these parts numbered from top to bottom, then S1 S2 S3 is equal to a = 1 Persamaan parabola y = ax 2 bx c adalah sebagai berikut y = x 2 – 4x c melalui titik (0,1) 1 = 0 2 – 4(0) c c = 1 Maka bisa dihitung y = x 2 – 4x 1 x p = b/2a = (4)/2(1) = 2 dan y p = (2) 2 – 4(2) 1= 5 Sehingga titik puncak parabolanya yaitu (2,5) Jadi jawabannya yaitu E Soal 4 (UN 08)

Graph Y X 7 X 3 Mathskey Com

Y=x^2-4x 1 parabola

Y=x^2-4x 1 parabola-We're going to explore the equation of a parabola y=a x 2 b xc for different values of a, b, and c First, let's look at the graph of a basic parabola y=x 2, where a =1, b =0, and c =0 Notice the graph opens up, the vertex is at x=0, and the yintercept is at y=0Find the area lying above xaxis and included between the circle $x^2y^2=8x$ and the parabola $y^2=4x$ Once I draw the figure, I know how to apply integration to this

Without Using Table Of Value Draw The Graph Of Y X 2 4x 5 Brainly In

The parabola y^2 = 4x and x^2 = 4y divided the square region bounded by the lines x = 4, y = 4 and the coordinate axes If S_1, S_2, S_3 are respectively the areas of these parts numbered from top to bottom, then S_1 S_2 S_3 is equal to31 Find the Vertex of y = x 2 4x12 Parabolas have a highest or a lowest point called the Vertex Our parabola opens up and accordingly has a lowest point (AKA absolute minimum) We know this even before plotting "y" because the coefficient of the first term, 1 , isStep 1 The xintercept occurs when y=0 So let's set y=0=x^24x1 Step 2 Now use the quadratic formula given as where a=1 b=4 and c=1 Step 3 Substitute above values in quadratic formula and you get the following Note the values of x where y=0 and observe them on the graph Also, note a quadratic equation is basically a parabola if the value of x are real numbers

Y = x2 − 4x 1 y = x 2 4 x 1 Rewrite the equation in vertex form Tap for more steps Complete the square for x 2 − 4 x 1 x 2 4 x 1 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 1, b = − 4, c = 1 a = 1, b = 4, c = 1 Consider the vertex form of a parabolaThe line x y = 1 intersects the parabola y^2 = 4x at A and B Normals at A and B intersect at C If D is the point at which line CD is normal to the parabola, then coordinates of D areIn a parabola that opens downward, the vertex is the maximum point We can graph a parabola with a different vertex Observe the graph of y = x 2 3 Graph of y = x 2 3 The graph is shifted up 3 units from the graph of y = x 2, Graph of y = (x 2) 2 1 Previous section Introduction and Summary Next page Graphing Parabolas page 2 Take

X2 4x −1 = 0 x2 4x = − 1 x2 4x 4 = − 1 4 = 3 (x 2)2 = 3 x 2 = ± √3 = ± 1732 x = 1732 − 2 = 0268 x = − 1732 − 2 = −3732 xAssume that the equation of the parabola is $$$ y=a x^{2} b x c $$$ Since the parabola passes through the point $$$ \left(1, 4\right) $$$ , then $$$ 4=a b c $$$ Since the parabola passes through the point $$$ \left(2, 9\right) $$$ , then $$$ 9=4 a 2 b c $$$Question Write an equation of the parabola in the graphing form f(x) = x2 4x 3 = O y = (x 2)2 – 1 y 3 = x² 4x O y = (x 1)2 2x 2 None of these This question hasn't been solved yet Ask an expert Ask an expert Ask an expert done loading

Unique Quadratic Equation In The Form Y Ax 2 Bx C

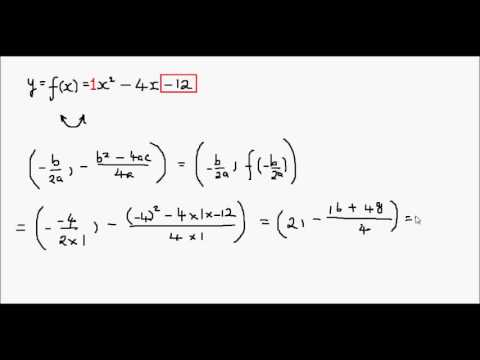
How To Sketch A Parabola Example 2 Y X 2 4x 12 Youtube

 Finding the yintercept of a parabola can be tricky Although the yintercept is hidden, it does exist Use the equation of the function to find the yintercept y = 12x 2 48x 49 The yintercept has two parts the xvalue and the yvalue Note that the xvalue is always zero So, plug in zero for x and solve for yEvery parabola has an axis of symmetry which is the line that divides the graph into two perfect halves On this page, we will practice drawing the axis on a graph, learning the formula, stating the equation of the axis of symmetry when we know the parabola's equationLet (x, y) be any point on the parabola y 2 = 4 x Let P be the point that divides the line segment from ( 0 , 0 ) to ( x , y ) in the ratio 1 3 Then the locus of P is

1

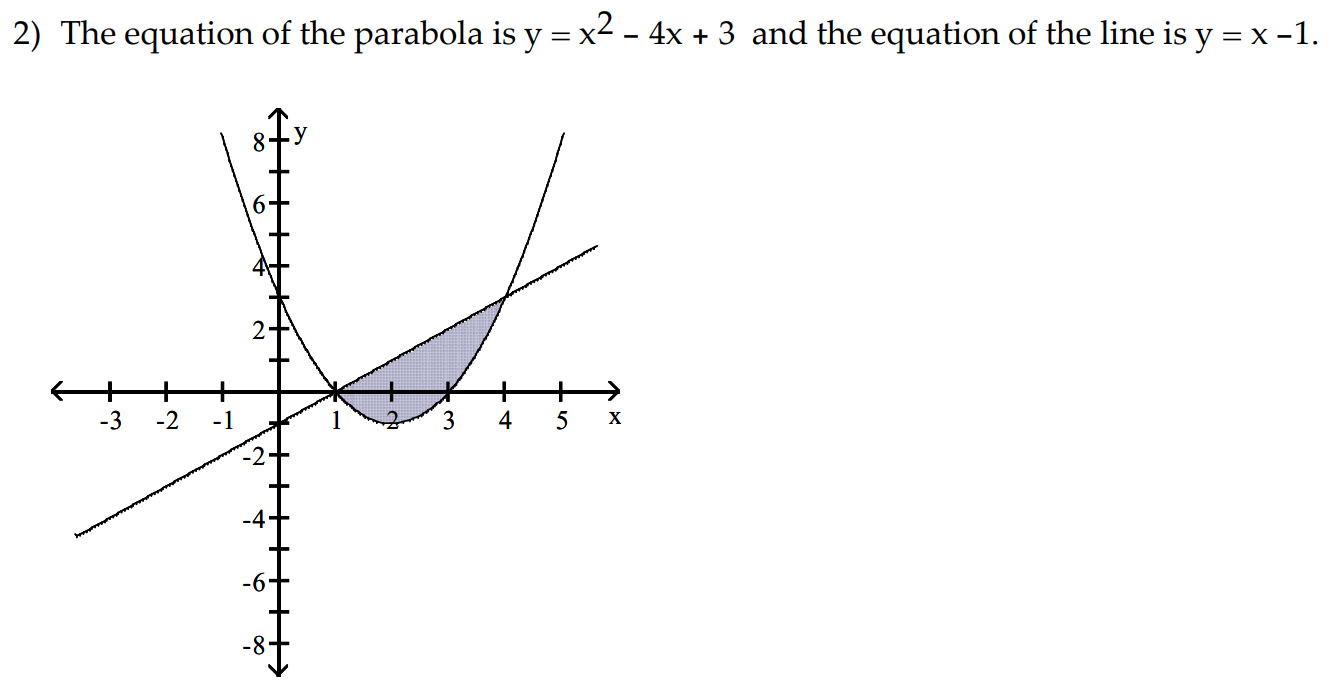
Solved 2 The Equation Of The Parabola Is Y X2 4x 3 Chegg Com

Then the equation of the shifted directrix is y1 = 2 or y=1 The picture illustrates the shift of the parabola from standard position to the new position Similarly, if we are given an equation of the form y 2 A y B x C=0, we complete the square on the y terms and rewrite in the form ( y k) 2 =4p( xWatch Video in App Continue on Whatsapp This browser does not support the video element The vertex is (2,4) Answer link Antoine Vertex is (2,4) Step 1 Complete the square y = − x2 − 4x = −(x − 2)2 −4 Step 2 Arrange so that you get the form (x −xv)2 = 4a(y − yv) y = − (x −2)2 −4 = −(x −2)2 4

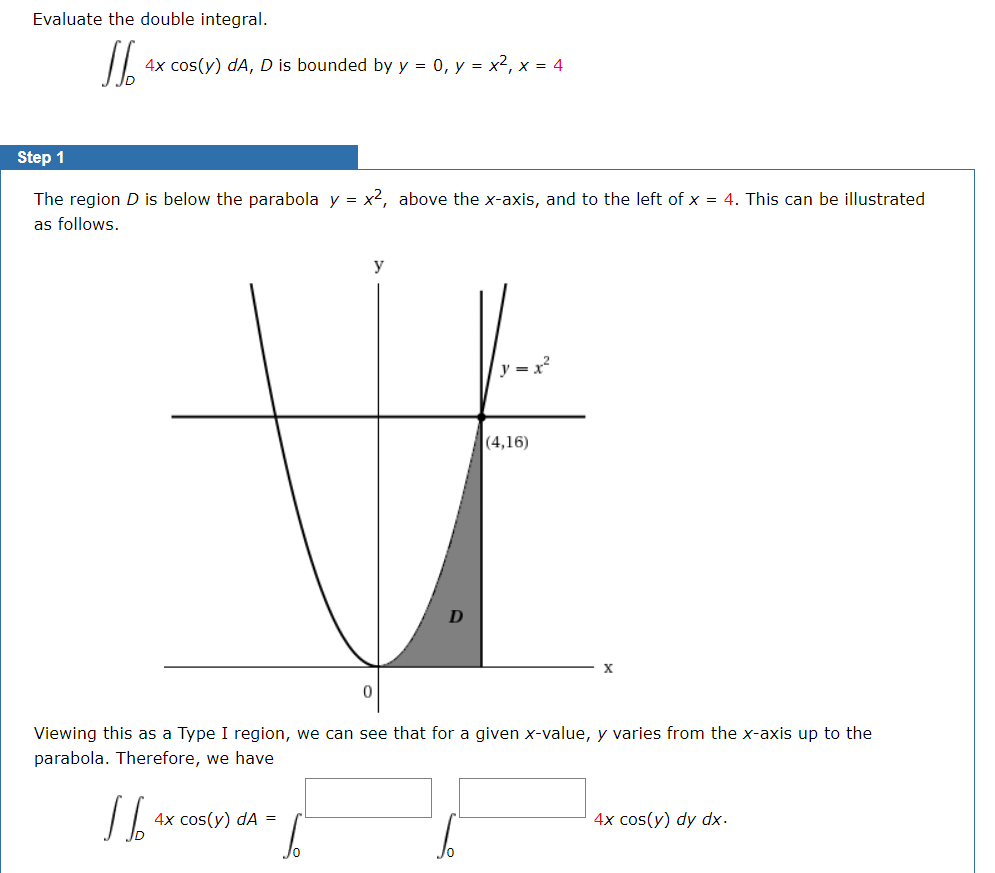
Solved Evaluate The Double Integral 4x Cos Y Da D Is Chegg Com

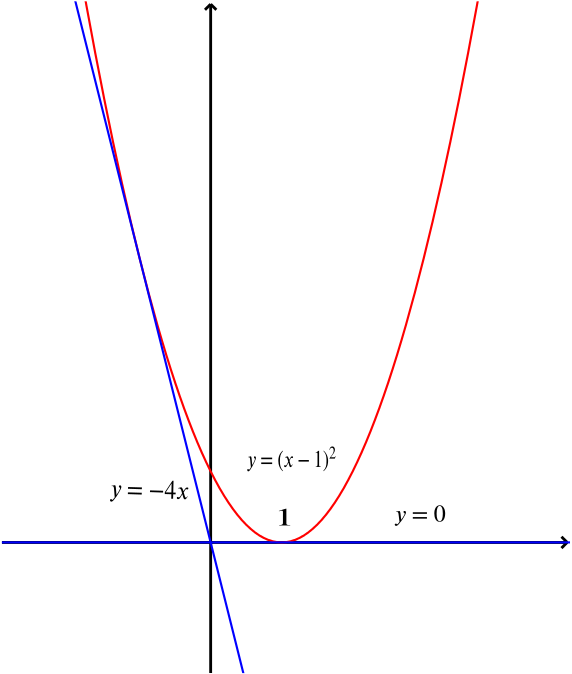
Solution When Does Y Kx Intersect The Parabola Y X 1 2 Quadratics Underground Mathematics

Algebra Calculator is a calculator that gives stepbystep help on algebra problems See More Examples » x3=5 1/3 1/4 y=x^21 Disclaimer This calculator is not perfect Please use at your own risk, and please alert us if something isn't working Thank you A circle touches the parabola y^2 = 4x at the point (1, 2) and also the directrix The ycoordinate of the pointAnswer to Find the following parabola's focus and directrix y = 4x^2 By signing up, you'll get thousands of stepbystep solutions to your

How Do I Graph The Quadratic Equation Y X 2 4x 6 Socratic

Manhassetschools Org

Given the parabola with standard equation {eq}y=x^24x5 {/eq} Then {eq}a=1, b=4, c=5 {/eq} Find the vertex using the vertex formula {eq}\begin{align} h&=\dfrac(1, 2) is on the parabola (2)(y)(y'(x) = 4 Gradient(slope) at (1, 2) = y'(1) = (2/2) = 1 Equation of the tangent line at (1, 2) is y 2 = (x 1) = x 1 => y x 1 = 0 Check (x 1)^2 = x^2 2x 1 = 4x => (x 1)^2 = 0 => x = 1A Free Quadratic simultaneous equation solver with steps When solving a system of linear and quadratic equations using an online solver, you need more than just the answers Our online calculator gives you a step by step solution for your system of equation

Find The Area Of The Region Bounded By The Parabola Y 2 4x The X Axis And The Lines X 1 And X 4 Sarthaks Econnect Largest Online Education Community

How Do You Find The Vertex Of Y 2x 2 4x Socratic

In completing the square, we will have y 2y 1 = 4x 8 1; Jose Camões Silva/Flickr/CC BY Find the line of symmetry of y = x 2 2x with 3 steps Find the vertex, which is the lowest or highest point of a parabola Hint The line of symmetry touches the parabola at the vertex(1,1)You don't have to sketch the curves to find the area, but it can help to see a picture of their graphs Now we need to find the points at which the curves intersect each other

Y X2 4x 6 Math Homework Answers

Graphing Solutions To Quadratic Equations Y X 2 4x 1 Youtube

If we are given a quadratic equation in which both x 2and y both occur with coe cient 1 then we can recover the equation for a circle by completing the square For example, suppose we are given the equation x2 4x y2 2y= 6 We can complete the square on x 2 4x, rewriting that as (x 4x 4) 4 = (x 2)2 4 and also The most general form of a quadratic function is, f (x) = ax2 bx c f ( x) = a x 2 b x c The graphs of quadratic functions are called parabolas Here are some examples of parabolas All parabolas are vaguely "U" shaped and they will have a highest or lowest point that is called the vertexExample Length of a Parabola a Figure 1 Arc length of y = x2 over 0 ≤ x ≤ a To find the arc length of a parabola we start with y = x2 y = 2x ds = 1 (2x)2 dx = 1 4x2 dx So the arc length of the parabola over the interval 0 ≤ x ≤ a is a 1 4x2 dx 0 This is the answer to the question, but it would be more useful to us if we

Parabolas

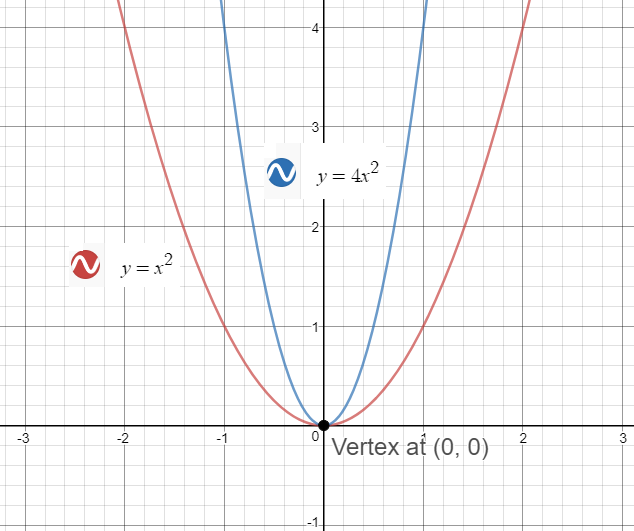
How To Graph A Parabola Y 4x 2 Socratic

Solutions to the Above Questions and Problems Solution The x intercepts are the intersection of the parabola with the x axis which are points on the x axis and therefore their y coordinates are equal to 0 Hence we need to solve the equation 0 = x 2 2 x 3 Factor right side of the equation (x 3) (x 1) () = 0 If line x2y1=0 intersects parabola y^(2)=4x at P and Q, then find the point of intersection of normals at P and Q Updated On 242 To keep watching this video solution for FREE, Download our App Join the 2 Crores Student community now! The parabola intercepts the xaxis when , then, you need to substitute into the equation Now, use the Quadratic formula In this case Substituting these values and evaluating, you get Remeber that Then, rewriting Simplifying Then The roots are complex, therefore, the parabola does not intercept the xaxis

Graph The Parabola Y 2x 2 4x 1 Youtube

The Parabola Below Is A Graph Of The Equation Y X 1 2 3 Mathskey Com

4x^ {2}4x1y=0 4 x 2 − 4 x 1 − y = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 4 for a, 4 for b, and 1y for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a} This equation is in standard form a x 2 b x c = 0Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeThe line of symmetry of y = 2x^2 4x 1 the axis of symmetry of x= b/2a, so the line of symmetry is x= 4/2x2= 1 x=1 the values of a, b, and c from the general form of the equation (2x 1)(x 2) =(2x 1)(x 2) = 2x²4xx2=2x²3x2=ax²bxc=0 by identifying, a =2, b=3 and c=2

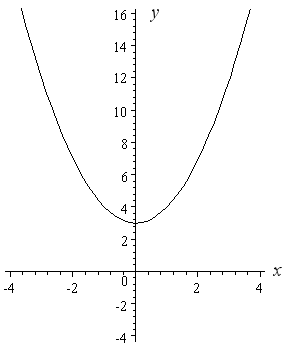
How To Draw Y 2 X 2 Interactive Mathematics

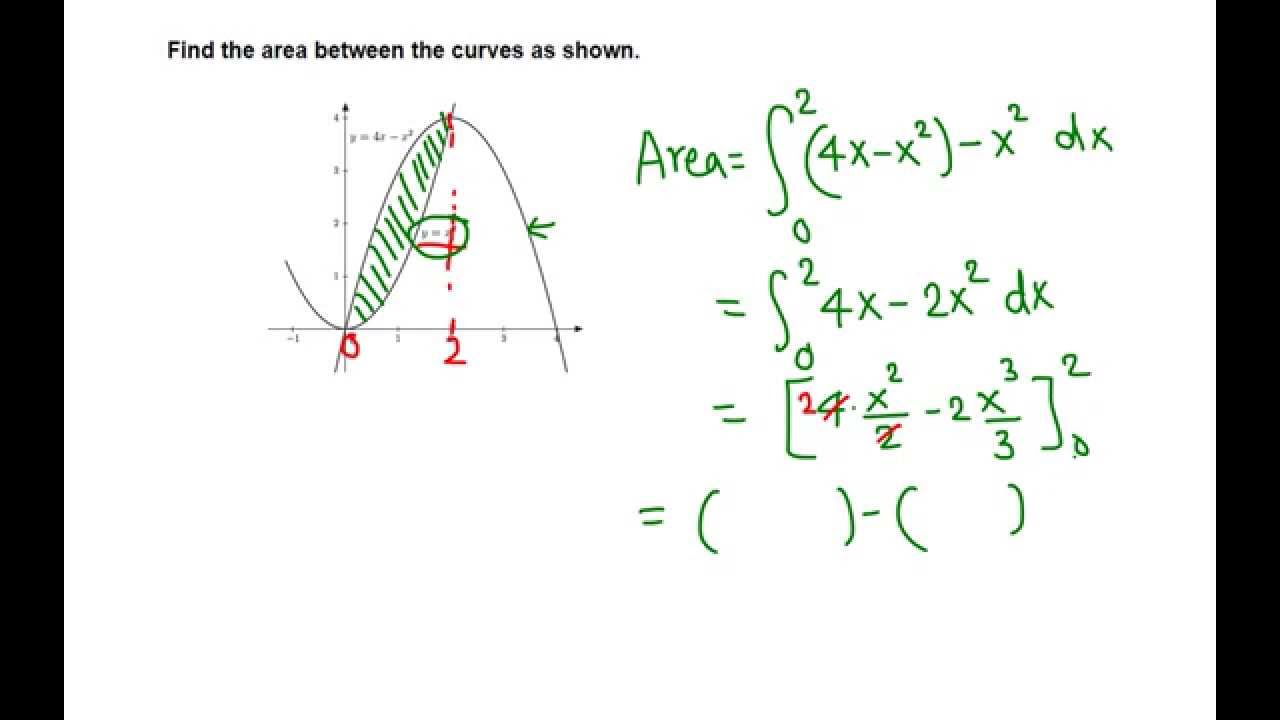
Area Between Y 4x X 2 And Y X 2 Youtube

Algebra > Quadratic Equations and Parabolas > SOLUTION Quadratic Equations Find the xintercepts of each parabolsc) y=x^24x4 d) y=4x^212x9 Thank you very much pleaseeeeeeeeeeee Log OnThis simplifies to (y 1) 2 = 4x 9 No matter how ugly the righthand side of the equation may get, we need to divide the right hand side by the coefficient of the x term (in this case, 4) This will leave us with (y 1) 2 = 4(x 9/4) From here we can say that the parabola will open to the left When we have the equation of a parabola, in the form y = ax^2 bx c, we can always find the x coordinate of the vertex by using the formula x = b/2a So we just plug in the values In this case, the equation in form y = ax^2 bx c is equal to y=x^2 4x 12

Parabola Sketching Y 2x 2 4x 6 From The Parabola Translation Download Scientific Diagram

Where Do Y X 2 4x 1 And Y 3 X Intersect Mathskey Com

Subtract y from both sides Subtract y from both sides x^ {2}4x1y=0 x 2 − 4 x 1 − y = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 4 for b, and 1y for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a} This equation is in standard form a x 2 b xFree Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experienceThe given equation of the parabola can be rewritten as (y1)^2 = 4 (x 9/4) Comparing this with the standard form (yk)^2 = 4a (xh) we have a = 1, h = 9/4, k = 1 Axis is y = k ie, y= 1 and latus rectum is x = ah ie, x = 1 9/4 or x= 5/4

Solution Graph The Parabola Y X2 4x 4 Use The Quadratic Formula To Solve The Equation To The Exact Value Or Round To Two Decimal Places 2x 2 X 1

Ch 5 Notes Ppt Video Online Download

What is the area of the region bounded by the parabola y^2=4x and the line x=1?Quadraticequationcalculator y=x^{2} en Related Symbolab blog posts High School Math Solutions – Quadratic Equations Calculator, Part 2 Solving quadratics by factorizing (link to previous post) usually works just fine But what if the quadraticThe Parabola Given a quadratic function f ( x) = a x 2 b x c, it is described by its curve y = a x 2 b x c This type of curve is known as a parabola A typical parabola is shown here Parabola, with equation y = x 2 − 4 x 5

Pcc Instructure Com

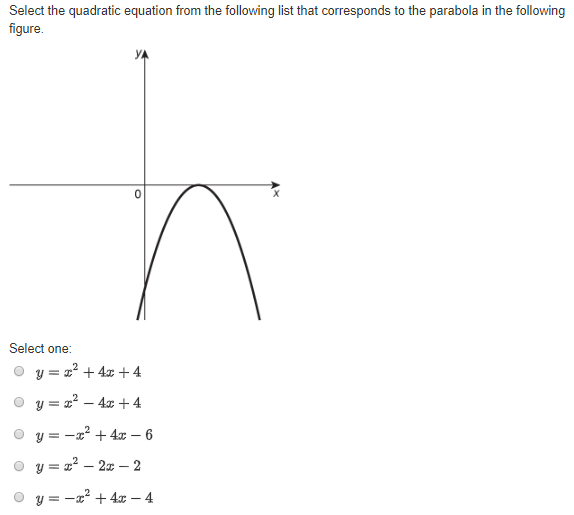
Solved Select The Quadratic Equation From The Following List Chegg Com

 At y = 0; y = x 2 4x 1 Compare it to standard form of parabola y = ax 2 bx c 1 Draw coordinate plane 2 Graph the line y = x 3 by using slope intercept form 3Draw the parabola y = x 2 4x 1 From the graph the intrsection points are (1, 4) and (2,5) answered by david ExpertI have an equation right here it's a second degree equation it's a quadratic and I know it's graph is going to be a parabola this was a review that means it looks something like this or it looks something like that because the coefficient on the x squared term here is positive and it's going to be an upwardopening parabola and I am curious about the vertex of this parabola and if I have

Solution Given The Quadratic Equation Y 2x 2 4x 1 Find The Coordinates Of The Vertex

Solution I Need Help To Solve This Problem And Graph It Y X 2 2 6

Graph y=x^24x1 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for The directrix of a parabola is the horizontal line found by subtracting from the ycoordinate of the vertex if the parabola opens up or downIn this video, we graph the trinomial / quadratic function y = x^2 4x 12 by finding its concavity, yintercept, using the turning point formulas and the

Y X 2 4x 32 Axis Of Symmetry 2 Vertex 2 36 X Intercepts 4 0 8 0 How Dose The Axis Of Symmetry Relate To Enotes Com

What Is The Vertex Of Y 2x 2 4x 12 Socratic

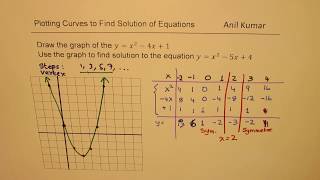
Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube

1 2 The Graphs Of Quadratic Equations

Tangents To Parabola Y 2 4 X 1 With Slopes In A Certain Range Determine Chords Bisected By X 1 Of A Circle Find The Equation Of The Circle Mathematics Stack Exchange

Graphing Quadratic Functions

How Do You Find The Vertex Of F X 2x 2 4x 6 Socratic

Y X2 Double Integral Of The Area Of The Y 4x X Region Homeworklib

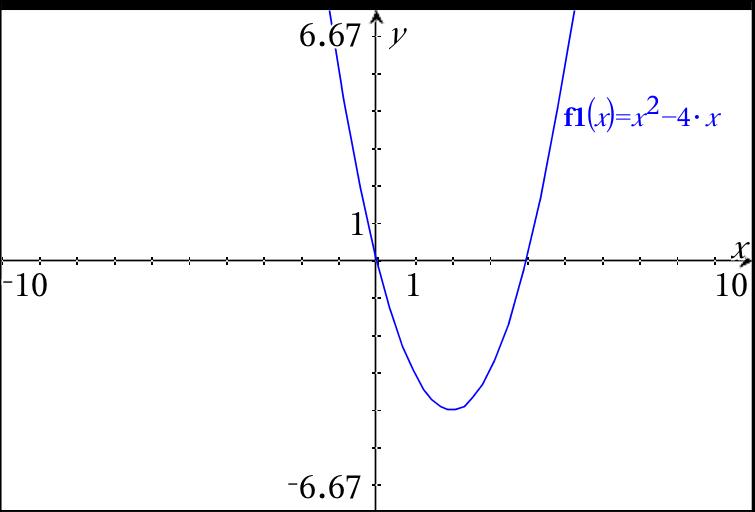
What Is The Graph Of F X X 2 4x Socratic

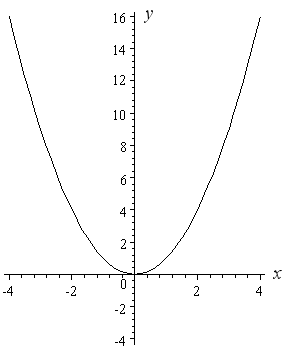
How To Draw Y 2 X 2 Interactive Mathematics

Plot A Graph For The Equation Y X 2 4x 1

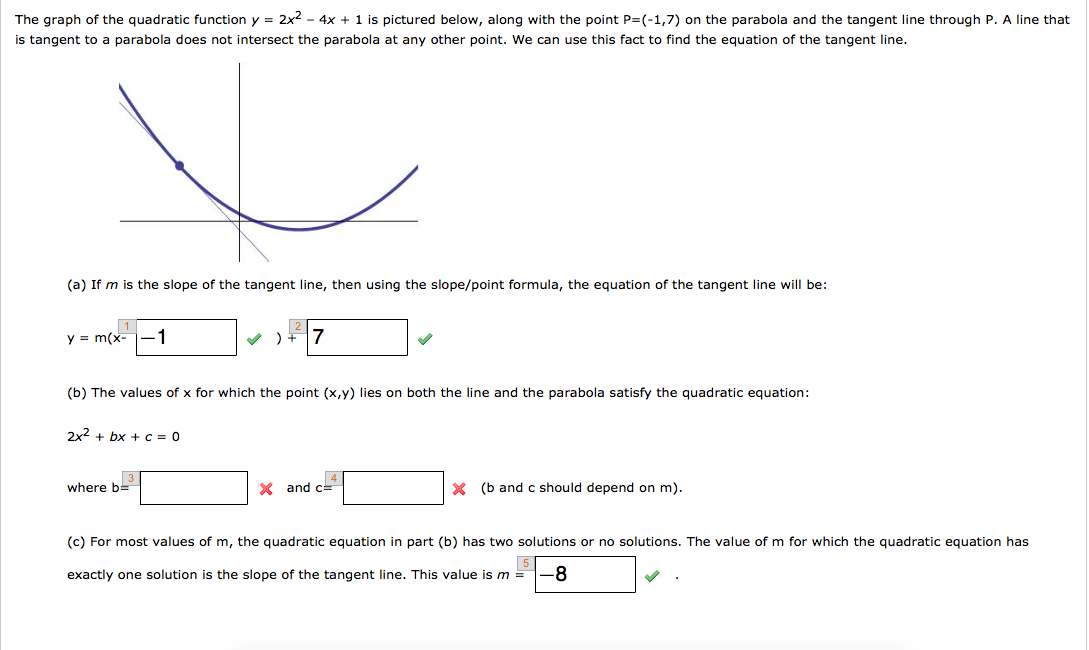
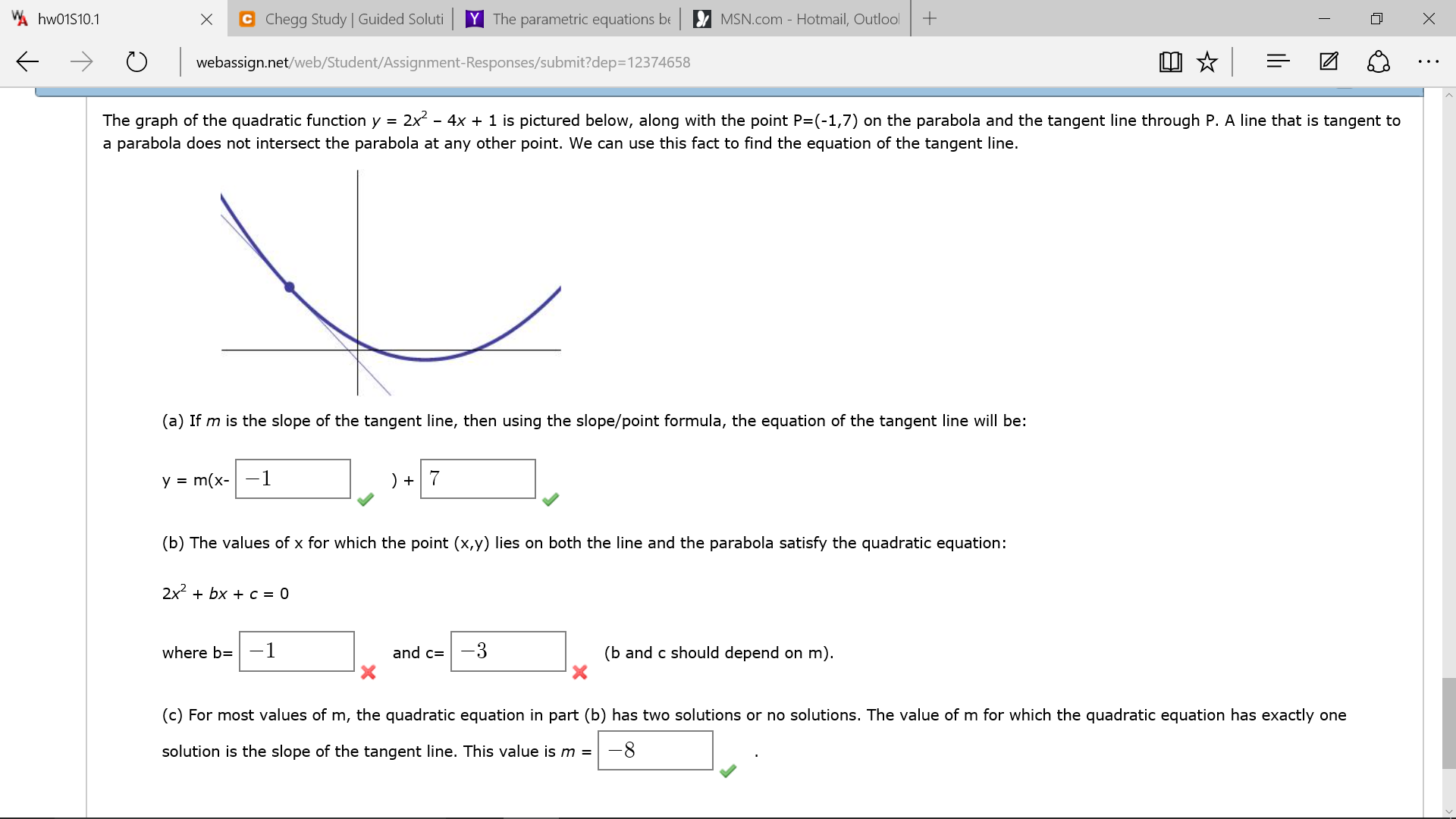
Solved The Graph Of The Quadratic Function Y 2x 2 4x 1 Chegg Com

Solution Find The Equation Of A Parabola That Has A Minimum Turning Point At 2 5 I Am Totally Confused How To Do This I Looked Up The Answer Which Is Listed As

Solution What Are The Coordinates Of The Turning Point Of The Parabola Whose Equation Is Y X 2 4x 1

Solved Consider Y 2x2 4x 1 This Equation Is Given In Chegg Com

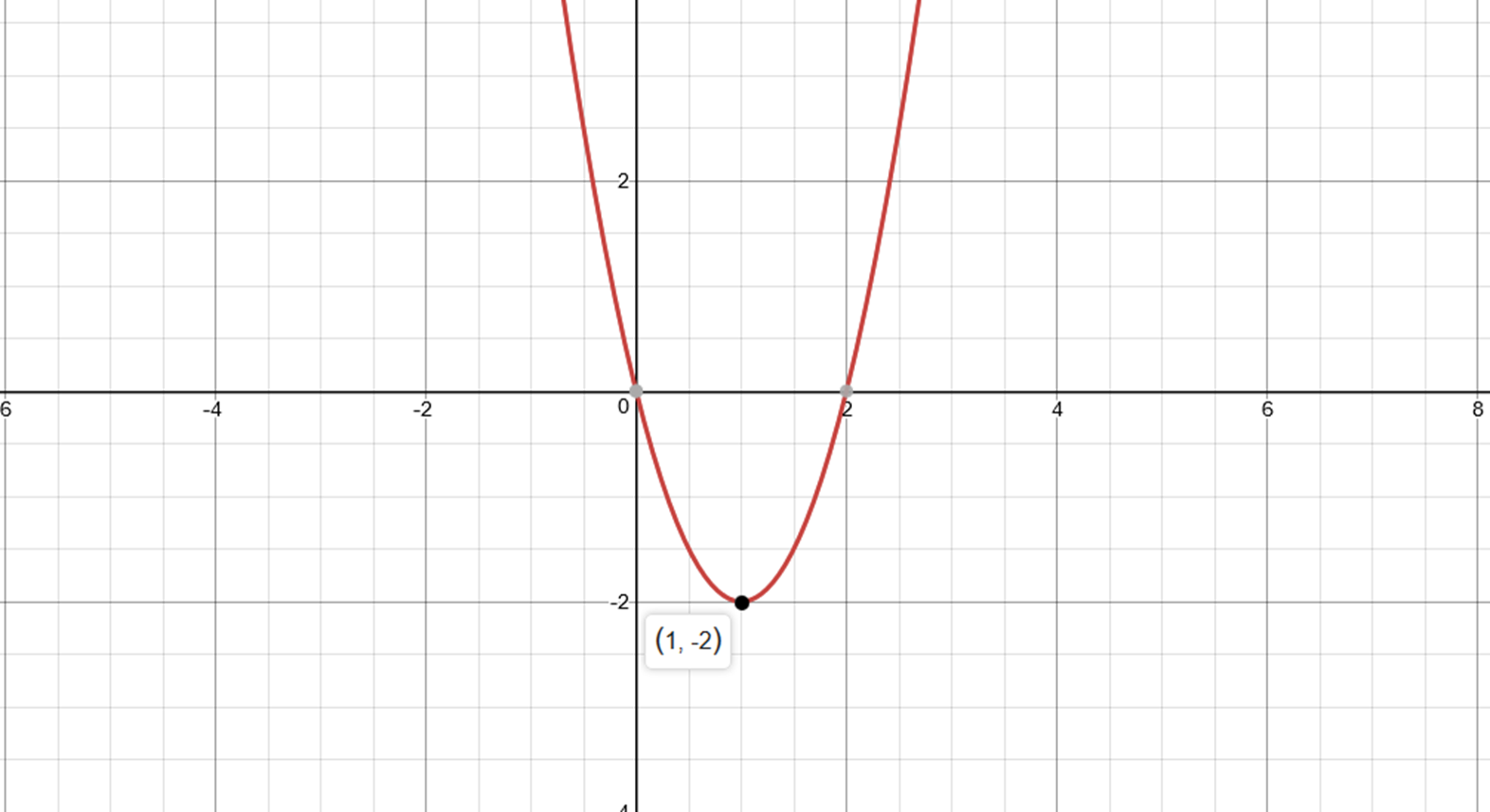
What Is The Vertex Of Y X 2 4x 1 Socratic

Analyzing The Parabola Ppt Download

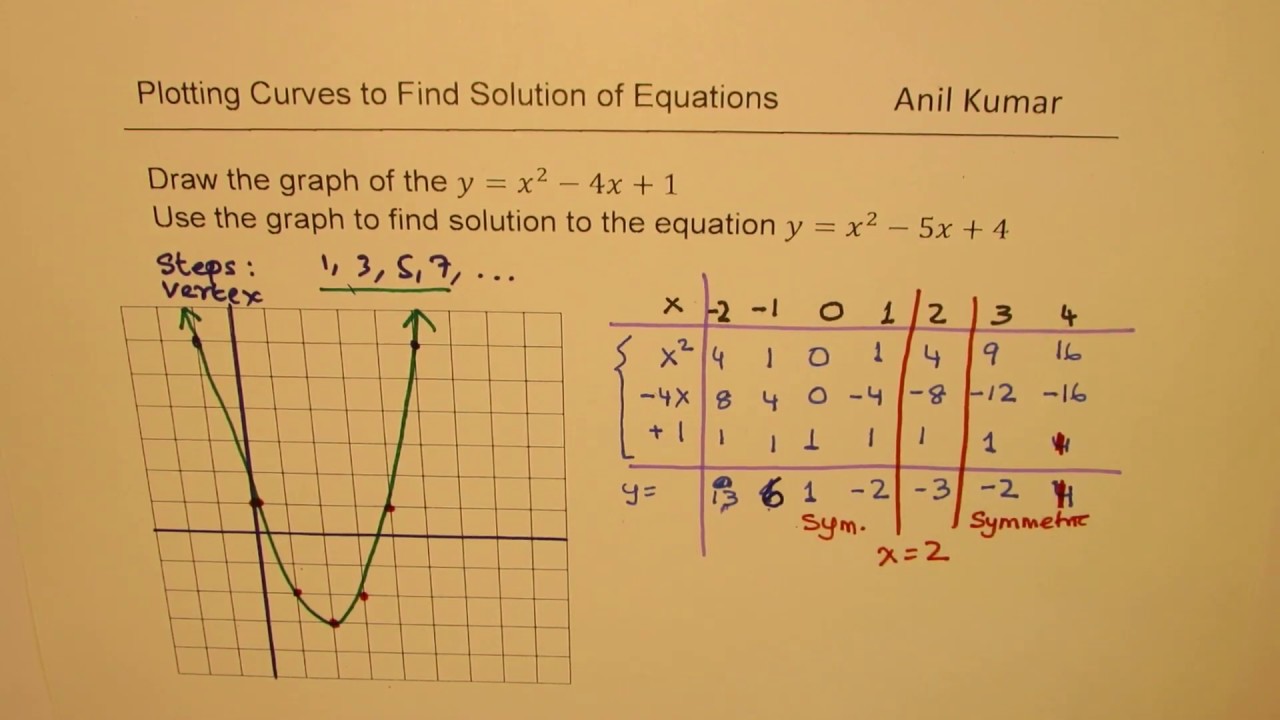
Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube

Tangents To Parabola Y 2 4 X 1 With Slopes In A Certain Range Determine Chords Bisected By X 1 Of A Circle Find The Equation Of The Circle Mathematics Stack Exchange

Consider The Parabola Whose Equation Is Y X 2 4x And The Line Y 2x B Then Whichfollowing Is Are Correct

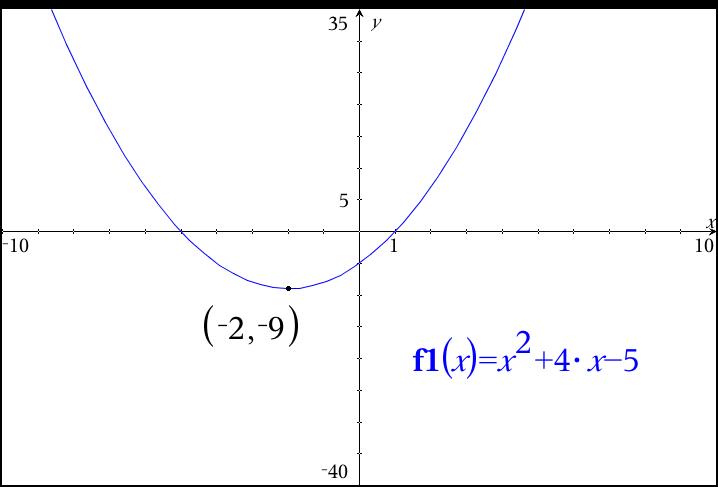
What Is The Vertex Of F X X 2 4x 5 Socratic

Exploration Of Parabolas

What Is The Area Of The Region Bounded By The Parabola Y 2 4x And The Line X 1 Quora

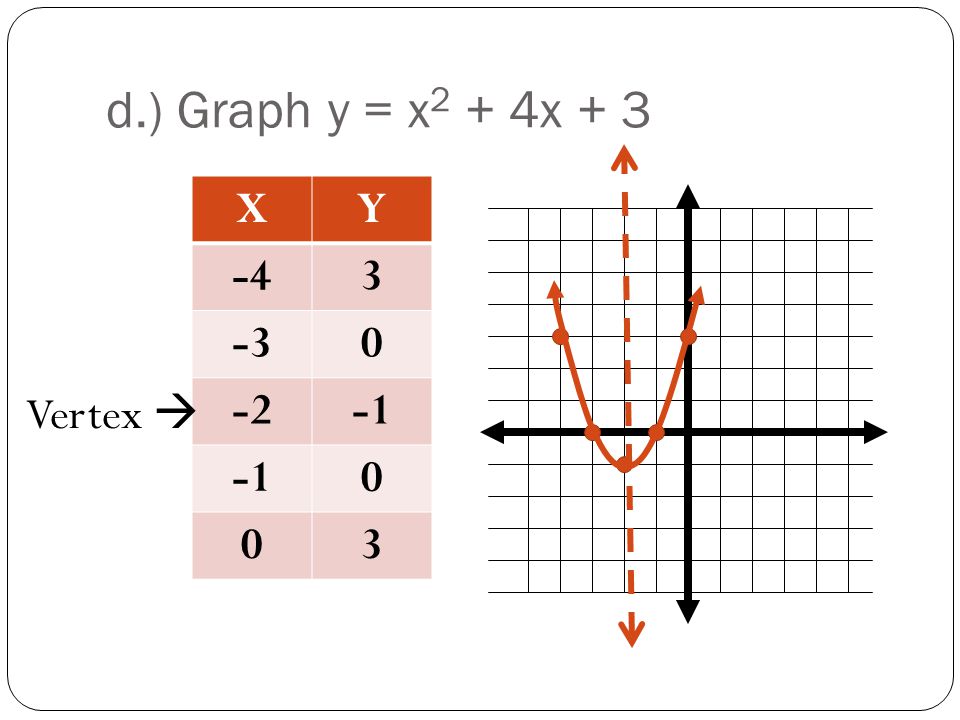
Solving Quadratic Equations By Graphing Ppt Video Online Download

The Area Bounded By The Parabola Y 4x 2 Y X 2 9 And The Line Y 2 Is A sqrt2 3 B 10sqrt2 3 C 40sqrt2 3 D Sqrt2 3

Solution Find The Coordinates Of The Vertex Of The Parabola

How Do You Graph Quadratic Functions Y X 2 4x 7 Socratic

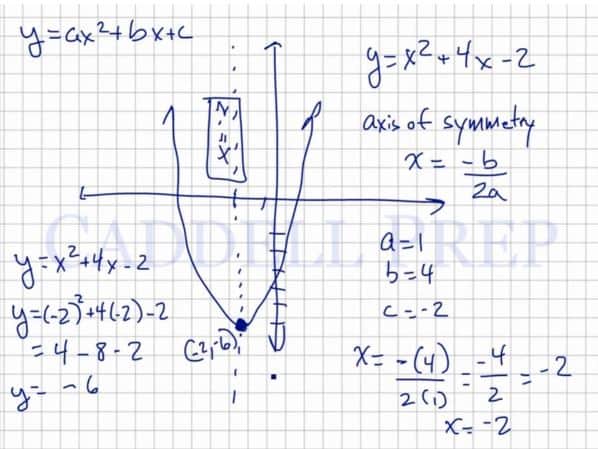
Learn About Properties Of Quadratic Functions Caddell Prep Online

Unique Quadratic Equation In The Form Y Ax 2 Bx C

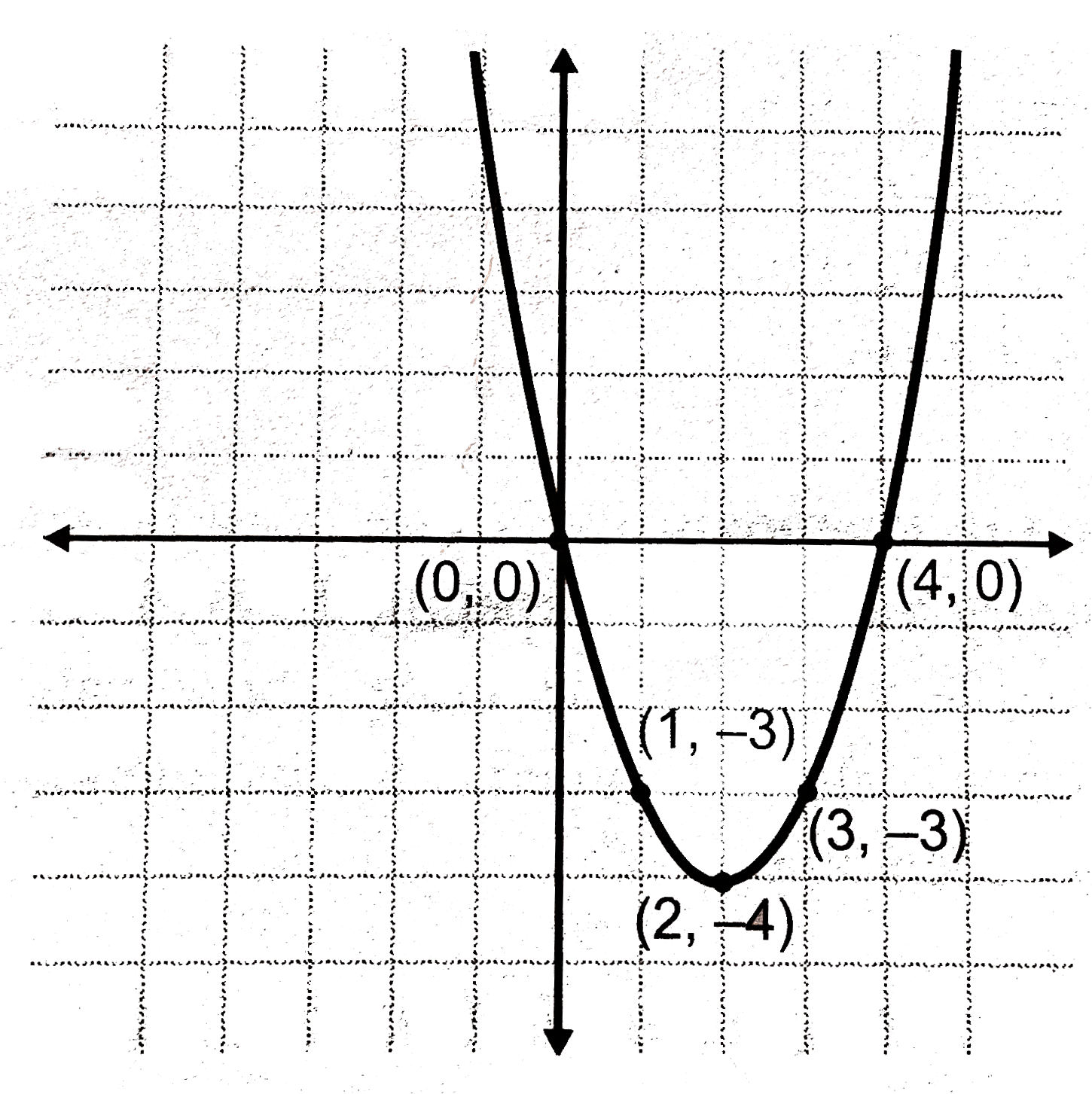
Plot A Graph For The Equation Y X 2 4x

Exploration Of Parabolas

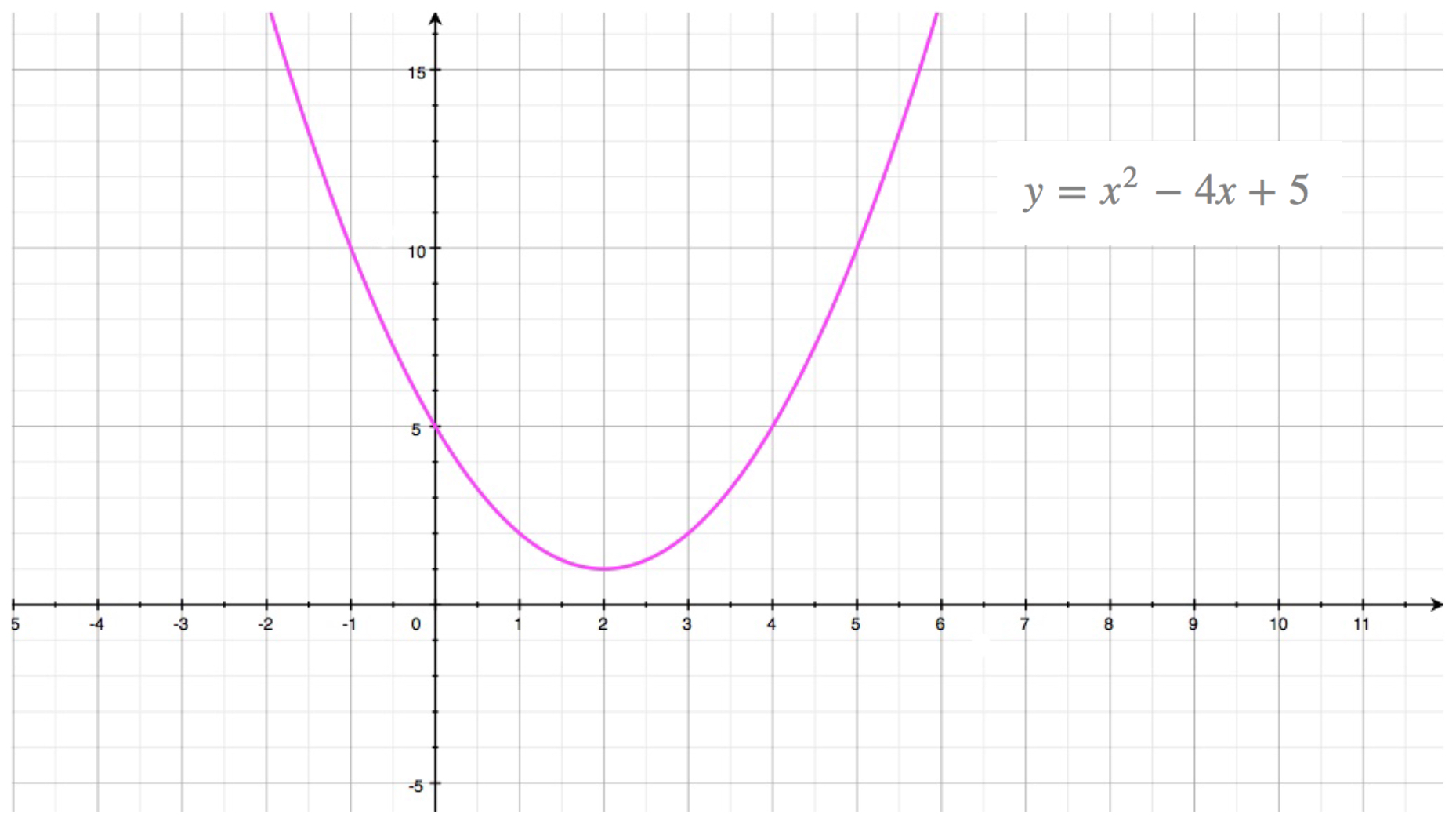
Quadratic Function Parabola

Solved 2 Hty 2 X 4 2 21 X 8 2 45 3o 31 3 2 하 Chegg Com

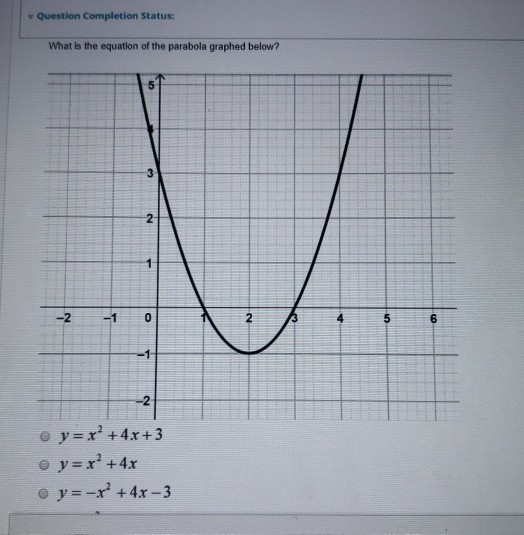
Solved Question Completion Status What Is The Equation Of Chegg Com

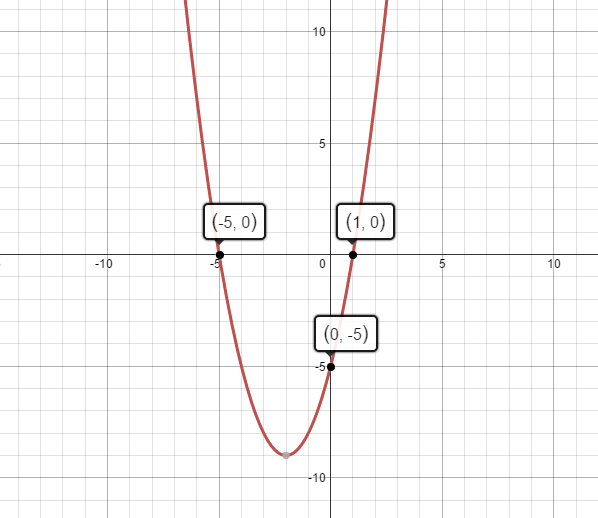
How Do You Factor Y X 2 4x 5 Socratic

Without Using Table Of Value Draw The Graph Of Y X 2 4x 5 Brainly In

1

Solution Use A Table To Graph They Function Y X 2 4 3 Ho Do U Graph It Including The Parabolas And Axis Of Symetry And The Vertex As A Maximum Or Minumum

Graphing Parabolas

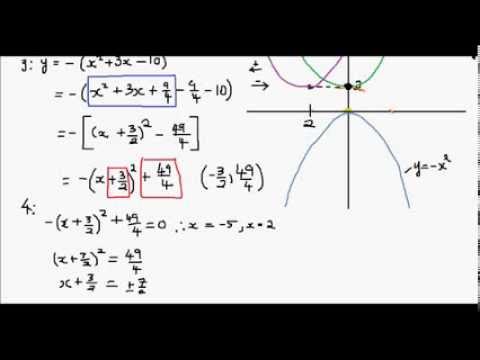
How To Sketch A Parabola Example 1 Y X 2 3x 5 Youtube

Ocr Mei Core 1 3 04 Sketch The Graph Of Y X 2 4x 4 Youtube

Graph The Parabola Y X 2 4x 1 Youtube

Completing The Square Solving Quadratic Equations 1 Express The Followings In Completed Square Form And Hence Solve The Equations X 2 4x 12 0 X Ppt Download

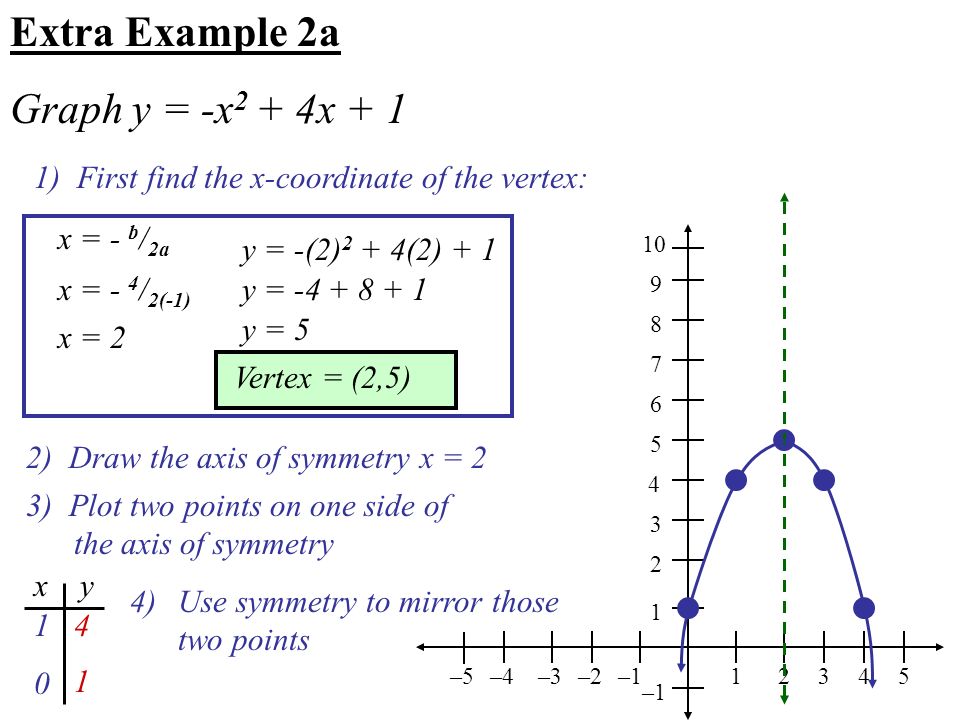
Ch 5 Notes Ppt Video Online Download

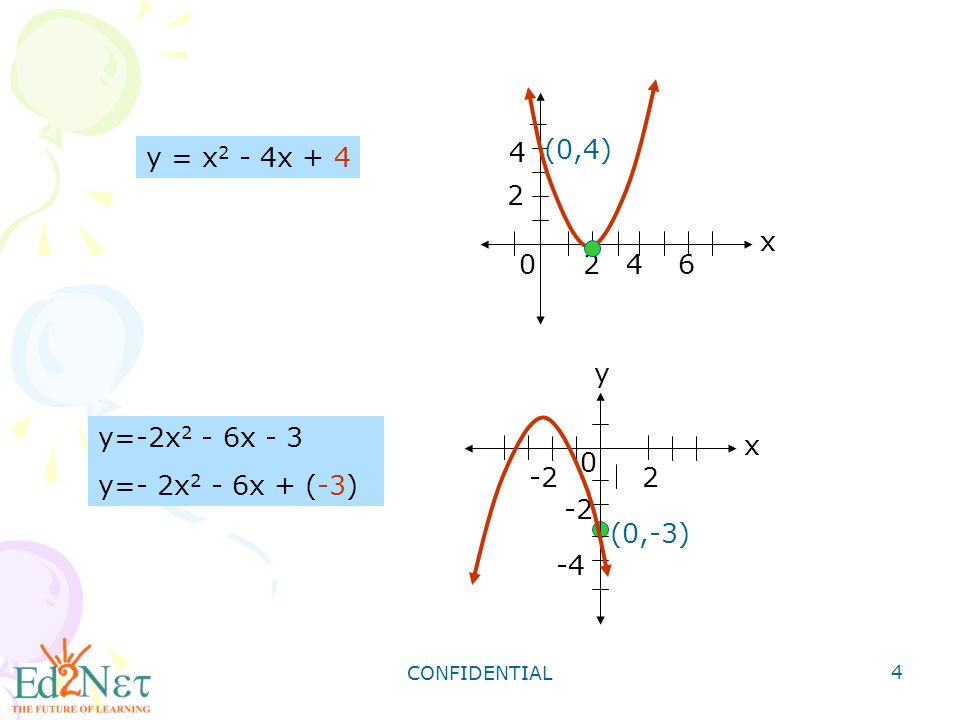
Confidential 1 Graphing Quadratic Functions Confidential 2 Warm Up Find The Vertex Of Each Parabola 9 Y X 2 4x 7 1 Y 5x X 3 2 Y Ppt Download

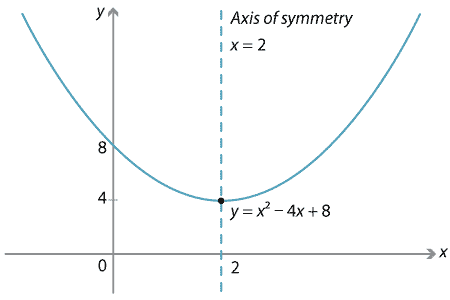
Content Transformations Of The Parabola

Graphing Quadratic Functions

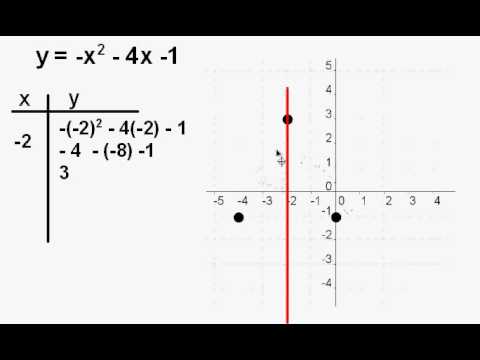
Graph The Parabola Y X 2 4x 1 Youtube

1

Y 4x 1 Slope

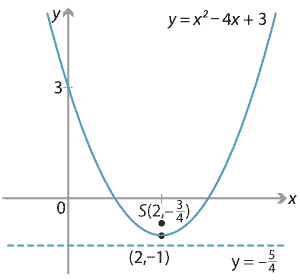
Content Focus Directrix Definition Of The Parabola

How Do You Find The Area Between The Curves Y 4x X 2 And Y X Socratic

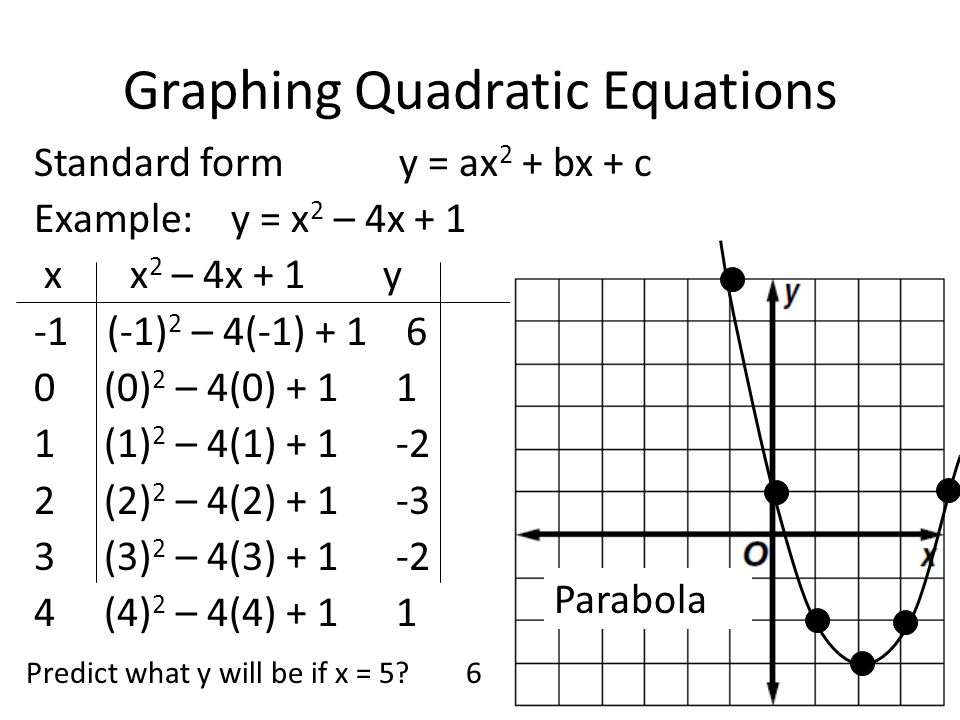
Graphing Quadratic Equations What Does A Quadratic Equation Look Like One Variable Is Squared No Higher Powers Standard Form Y Ax 2 Bx C Y X Ppt Download

Solved Use The Information Provided To Write The Vertex Form Chegg Com

Graph Y X 7 X 3 Mathskey Com

Find The Area Of The Region Bounded By The Parabola Y 2 4x The X Axis And The Lines X 1 And Youtube

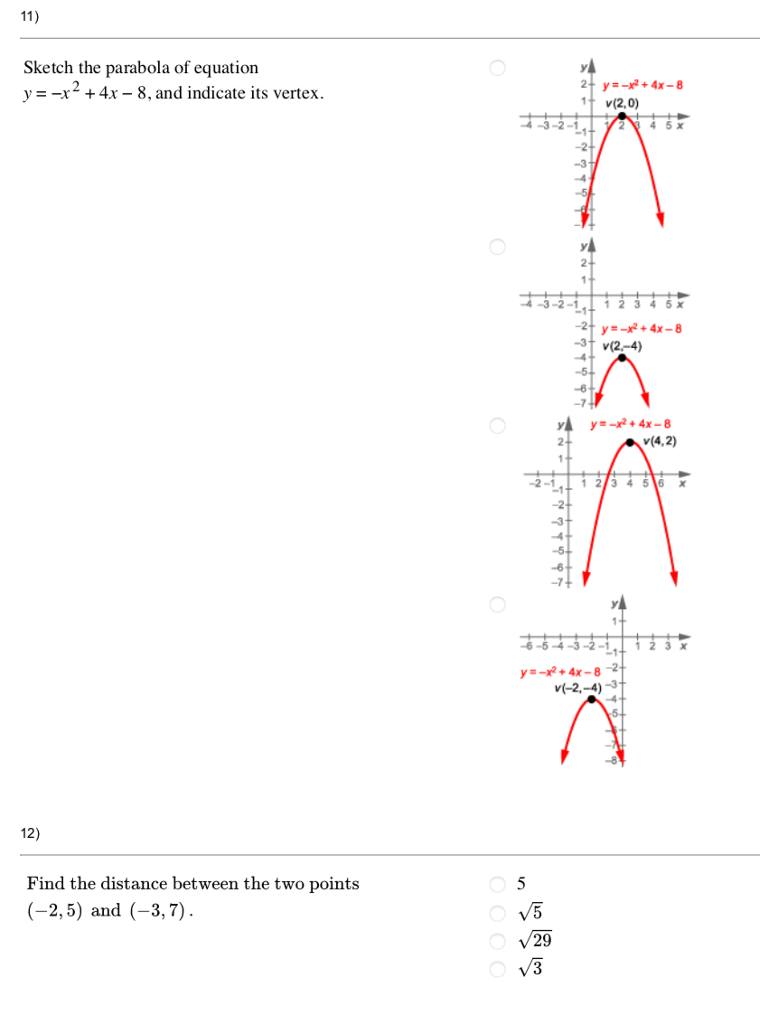
Solved 11 Sketch The Parabola Of Equation Y X 4x 8 And Chegg Com

Solution Find The Coordinates Of The Vertex Of The Parabola

How Do You Graph Y 2x 2 4x 3 Mathskey Com

The Point On The Curve Y X 2 4x 3 Which Is Closest To The Line Askiitians

Let S Learn Standard Form

Solved 5 Write The Equation Of The Parabola In Vertex Form Chegg Com

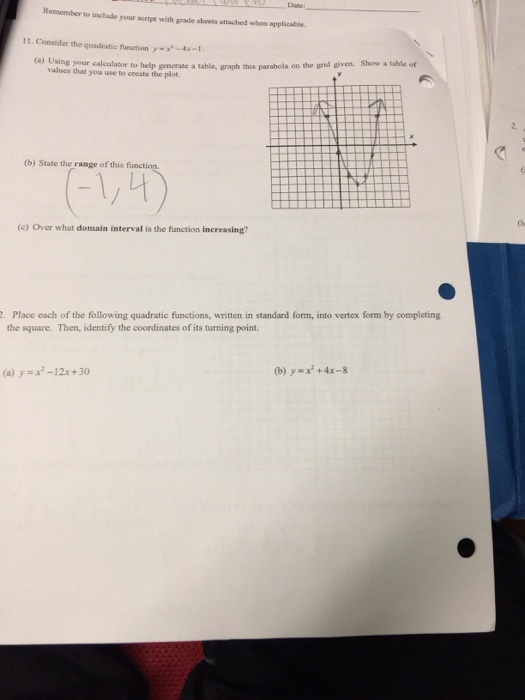
Solved Consider The Quadratic Function Y X 2 4x 1 Chegg Com

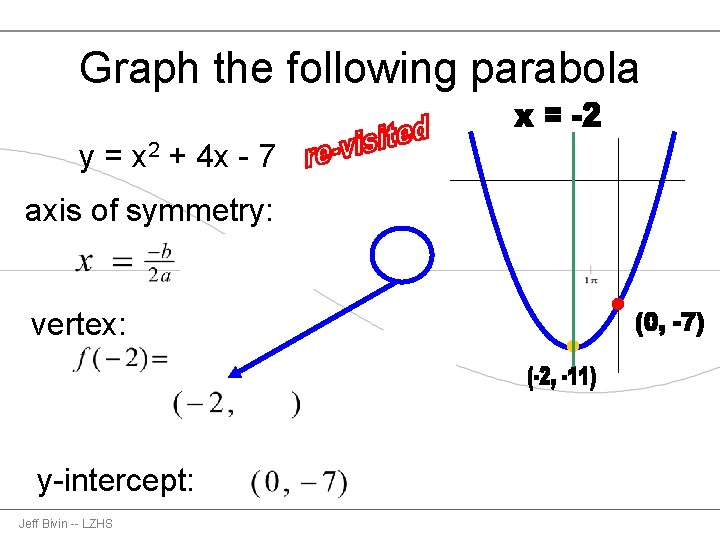
Graphing Parabolas Using The Vertex Axis Of Symmetry

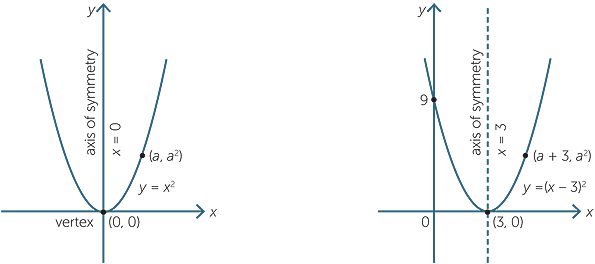
Quadratic Function

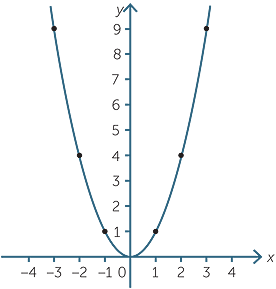
Quadratic Function

Solution Find The Coordinates Of The Vertex Of The Parabola Y X2 4x 1 By Making Use Of The Fact That At The Vertex The Slope Of The Tangent Line Is Zero

Graphing Parabolas

Solution Write Each Function In Vertex Form Sketch The Graph Of The Function And Label Its Vertex 33 Y X2 4x 7 34 Y X2 4x 1 35 Y 3x2 18x 36 Y 1 2x2 5x

2 02 Quadratic Equations

How Do You Find The Vertex Directrix And Focus Of X 2 4x 4y 16 0 Socratic

Solved The Graph Of The Quadratic Function Y 2x 2 4x 1 Chegg Com

Quadratics Graphing Parabolas Sparknotes

How To Find Quadratic Line Of Symmetry

Solution Find The X Intercepts Y X 2 4x 32

How Do You Graph Y 2x 2 4x 3 Mathskey Com

What Is The Equation Of The Tangent To The Parabola Y 2 4x At The Point 1 2 Quora

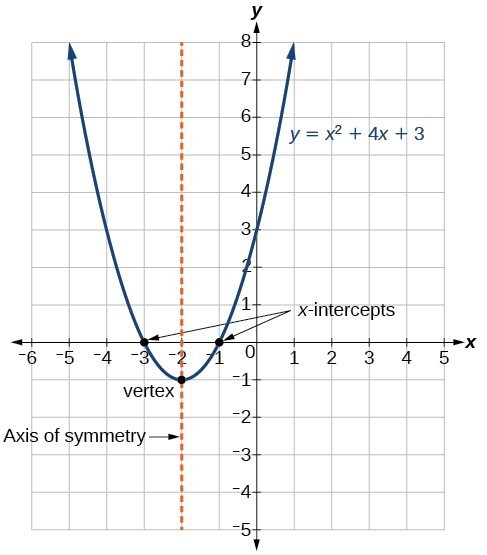
Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra